The Canadian banks have very low reserves-to-loans ratios (“reserve ratios”). Why? The banks are generally restricted by accounting rules from setting aside specific reserves until after there has been some form of impairment/loss event (often referred to as an “incurred loss” model). This makes it very difficult for the Canadian banks to set aside allowances/reserves for impaired loans in advance of loans going “bad”. The result, given that the sector has – for now – extremely good asset quality, is that the banks also have very low reserve ratios compared to U.S. banks, global banks and their own recent history. In this Insight, we discuss why we believe the abrupt rise in loan losses in Q1, combined with very low reserve ratios, is increasing the potential for the banks to build reserves through the rarely used sectoral allowances.
- Part #1: Canadian Banks – Are Sectoral Allowances the Solution to Low Reserve Ratios?
- Part #2: Canadian Banks – How Worried Should You Be (about Rising Loan Losses, Low Reserve Ratios, and Recessionary Alberta)?
- Part #3: Canadian Banks – Are Falling Global Reserve/Capital Rankings Increasing Regulatory Risk?
Highlights
- Constrained by Accounting, Canadian Banks Have Very Low Reserve Ratios: The banks are generally restricted by accounting rules from setting aside specific reserves against performing loans expected to go “bad” until after there has been some form of impairment event. Therefore, because the banks currently have excellent asset quality, their reserves-to-loans ratios remain well below historical averages.
- Rising Provisions from Energy/Alberta Likely in Coming Quarters: With the Canadian banks having over $100 bln in drawn/undrawn exposure to the energy sector, and 20% of the Canadian economy (Alberta) in a recession, it is our view that the probability of rising loan losses placing upward pressure on reserve levels, possibly in the form of rarely used sectoral allowances, is increasing.
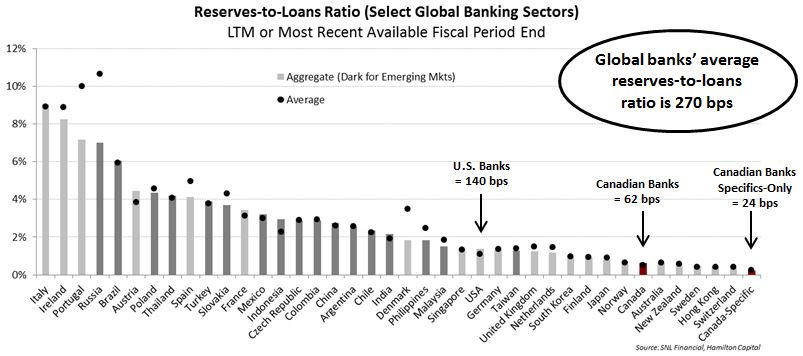
- Canadian Bank Reserve Ratios Low Relative to Recent History and Global Peers: At just 62 bps, the Canadian banking sector’s reserves-to-loans ratio is one-quarter the level of its global peers (average for 39 countries is ~270 bps), U.S. banks (~140 bps), and its own 15 year average (~100 bps).
- Potential for Rarely Used Sectoral Allowance Build Rising Materially: Media speculation is that OSFI is pressing the banks to raise reserves against their oil and gas portfolios. If true, we believe the probability that Canadian banks book sectoral allowances in order to increase reserves rapidly is rising. Depending on the size, sectoral allowances could help alleviate investor concerns over low reserve ratios. That said, it is difficult to anticipate the potential market reaction, particularly if investors are not convinced that the reserve build definitively accounts for future losses. Low reserve levels and possible regulatory pressure have the potential to create uncertainty for equity investors.
Note to Reader:
“Allowances” and “Reserves” are used interchangeably in this note. The former is the dominant term for Canadian banks, while the latter is more commonly used for U.S. banks. In this note, we refer to sectoral allowance accounting during a period in which it was allowed under Canadian GAAP. However, under the current IFRS accounting, there is no specific reference to sectoral allowances. That said, it is commonly understood that current accounting rules do not prevent the establishment of allowances that have the same effect as what a sectoral allowance under Canadian GAAP would have achieved; i.e., an allowance for industry sectors and geographic regions that have experienced specific adverse events or changes in economic conditions, where an additional allowance for loan loss for groups of loans as a whole, even though the individual loans comprising each group are still performing. Therefore, for clarity and ease of understanding, we have adopted the previous Canadian GAAP vernacular.
With the more than 50% decline in the price of oil and Alberta (representing ~20% of the Canadian economy) in the second year of a recession, the Canadian banking sector’s very low reserve ratios are becoming a concern for investors, particularly since the banks saw a ~20% rise in provisions for credit losses last quarter. With over $100 bln in drawn/undrawn exposure (i.e., ~$50 bln drawn; ~$57 bln undrawn) to the energy sector, and over $100 bln of uninsured retail loans to Alberta, the Canadian banks face the risk of further deterioration in asset quality (i.e., increasing gross impaired loans).
It is our view that the combination of very low reserve ratios and the sharp rise in provisions last quarter is increasing the probability that the Canadian banks will seek to raise reserves (possibly materially) in the upcoming quarters. In addition, although their usage is relatively rare, we believe there is an increasing probability that the banks will seek to build reserves through the recording of material sectoral allowances against their energy portfolios.
How Low are Canadian Banks’ Reserve Levels? Sector Ranks Near the Bottom of Global Banks
As the chart below highlights, the average reserves-to-loans ratio of the thirty-nine countries listed is ~270 bps[1]. This compares to the Canadian banks at just 62 bps, or one-quarter the level of their peers, putting the sector close to last among global banks[2]. While many, if not most, of these countries have inferior asset quality, it is difficult to reconcile the magnitude of this difference, given the aforementioned exposures to oil and gas firms, specifically, and the fact that 20% of the Canadian economy is in a recession (i.e., Alberta). It is also worth noting that ~60% of Canadian bank reserves are in the form of general allowances[3], which, given the fact these reserves are extremely difficult to draw down in any significant way against portfolio impairments, compromises the quality of Canadian bank reserves. Hence, we believe investors should focus more on specific reserve levels, which are even lower.
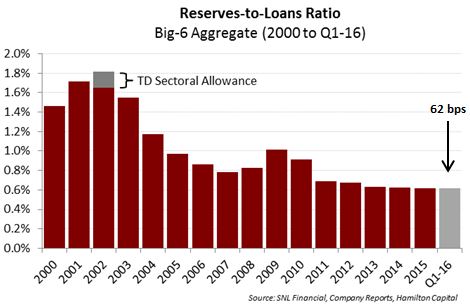
Not only are Canadian bank reserves low relative to their global peers, they are also low relative to the sector’s recent past. For example, the 15 year average for this ratio is ~100 bps, and the current ratio is among the lowest during this same period when it reached as high as ~170 bps (in 2001, excluding TD’s sectoral allowance in 2002).
Regulatory Risk on the Rise; Higher Probability of Sectoral Allowances for Energy Portfolios
Under the previous Canadian GAAP, sectoral allowances were rare, and we know of only two instances where a Canadian bank booked a material sectoral allowance: TD’s very significant ~$1.5 bln sectoral allowance, primarily against its telecom portfolio in 2002[4]; and BNS’s $60 million against the auto sector in 2009. In its 2002 annual report, TD described its sectoral allowance as follows:
“We have established sectoral allowances for credit losses for industry sectors and geographic regions that have experienced specific adverse events or changes in economic conditions. In these cases it was necessary to establish an additional allowance for loan loss for groups of loans as a whole, even though the individual loans comprising each group are still performing.” [5]
The recording of sectoral allowances for Canadian bank energy exposures has the potential to alleviate some of the growing concerns investors have regarding the low reserve ratios relative to prior years and to their U.S. and global banking peers. Given that the price of oil remains relatively low (even with the recent rally), we believe the potential for large and immediate reserve builds under this accounting treatment is becoming increasingly likely.
The challenge in estimating the necessary reserves for the banks’ sizeable energy portfolios is that, by definition, a key assumption is the price of oil over the life of the loan, which is very difficult to predict accurately. Therefore, we can see a situation where the Canadian banks assume a partial rebound in the price of oil in the first estimate, and then further build this reserve if oil remains below the original assumption for a sustained period of time. Returning to TD as an example, the bank booked $870 mln in Q3 2002, before booking a further $600 mln in Q4. It then drew down this reserve over the next two years.
With limited precedent, it is difficult to anticipate the market reaction if the banks book sectoral allowances, particularly en masse. As noted, although TD’s first estimate of the necessary sectoral allowance in Q3 2002 was substantial at $870 mln, it still needed to increase the reserve materially the very next quarter. So, it is possible that the market views the initial booking of a sectoral allowance more as an acknowledgement of higher losses to come rather than concluding that the credit issues from energy have been dealt with definitively.
It is worth noting that TD’s share price underperformed the Canadian bank index by over 6% in the six months that followed its initial announcement of sectoral provisions in July 2002. From a market perspective, we believe a gradual approach to sectoral allowances would be less preferable to a very large “one and done” reserve build, as it has the potential to create earnings uncertainty for several quarters.
Not only are total reserve ratios lower for the Canadian banks than their U.S. peers, but the reserves set aside against the Canadian banks’ energy portfolios are also substantially below those of the U.S. banks. Reserve ratios also appear to be well below conservative estimates of cumulative losses given the current price of oil. With press reports that OSFI is expressing a desire for the banks to raise their energy reserves[6], we believe it is becoming increasingly likely the Canadian banks will book sectoral allowances in order to raise reserves rapidly with the blessing of the regulator. Of course, it is not clear if each bank’s view of reserve sufficiency will be the same as OSFI’s, and if global bank investors have learned anything in the past eight years, it is that regulatory risk is difficult to quantify.
We believe in aggregate this has the potential to create additional uncertainty for equity investors over the next several quarters.
Notes
[1] Our global banking statistics are measured on a universe of banks that includes all publicly-traded banks defined and covered by SNL Financial LC with market capitalizations exceeding US$300 million, as of September 2015. As a result, some aggregate data for a particular country or region may not be the same as government reported data for its domestic sector.
[2] It is also worth noting that several of the countries/banks with lower reserve-to-loan ratios than the Canadian banks – i.e., Sweden, Hong Kong, and Switzerland – have higher regulatory capital levels. For example, the average common equity tier 1 ratio of the “Big-4” Swedish banks is nearly 20%, double that of Canada’s “Big-6” average of closer to 10%.
[3] “General” refers to “collective allowance on unimpaired loans”.
[4] TD booked sectoral provisions of $1,470 million in 2002, ending the year with a sectoral allowance of $1,285 million after $205 million was transferred to specific allowance.
[5] It also added “Sectoral allowances are computed quarterly, on a portfolio basis, taking into account the expected loss of the portfolio of borrowers in the sector under review. The analysis includes a review of probabilities of default, loss given default and exposure at default. The results of the analysis are compared to the level of general allowances allocated to the portfolio using the general allowance methodology with any excess requirement included in the sectoral allowances.”
[6] The Superintendent of Financial Institutions was quoted, stating: “We want them to take a good look at its accounting practices”. When referring to reserves, the Superintendent also noted “They should support loss-absorbing capacity and the ability to manage through difficult times in general.”